Principal Component Analysis (PCA)

PCA betreft een wiskundige techniek die wordt gebruikt om de dimensie van datasets te reduceren. Het doel is om complexe datasets eenvoudiger te maken door de belangrijkste kenmerken, ook wel principale componenten genoemd, te identificeren en te behouden, terwijl de minder belangrijke informatie wordt verwijderd.

Hoe werkt de PCA?

1. Data Normalisatie
   PCA begint met het normaliseren van de data. Dit betekent dat alle kenmerken (features) worden geschaald, zodat ze dezelfde eenheid hebben (gemiddelde = 0 en standaardafwijking = 1). Dit is belangrijk omdat PCA gevoelig is voor schaalverschillen.
   
2. Covariantiematrix Berekenen
   Vervolgens wordt de covariantiematrix van de dataset berekend. Deze matrix beschrijft hoe verschillende kenmerken met elkaar samenhangen.
   • Positieve covarianties: kenmerken hebben een positieve correlatie.
   • Negatieve covarianties: kenmerken zijn negatief gecorreleerd.
     
3. Eigenwaarden en Eigenvectoren Bepalen
   Uit de covariantiematrix worden de eigenwaarden en eigenvectoren berekend.
   • Eigenwaarden: Geven de variatie weer die door een bepaalde component wordt verklaard.
   • Eigenvectoren: Bepalen de richting van de principale componenten.
     
4. Principale Componenten Selecteren
   De eigenvectoren worden gerangschikt op basis van hun bijbehorende eigenwaarden. De eerste paar eigenvectoren met de grootste eigenwaarden worden gekozen als de principale componenten.
   
5. Projectie op een Lagere Dimensie
   De originele data wordt getransformeerd en geprojecteerd op de geselecteerde principale componenten. Dit resulteert in een dataset met minder dimensies.

Belangrijke Concepten

• Principale Componenten (PC’s): Lineaire combinaties van de oorspronkelijke kenmerken die de maximale variantie in de data verklaren.
  • PC1: De richting met de grootste variantie in de data.
  • PC2: De volgende orthogonale richting met de grootste resterende variantie.
• Uitleg van Variantie: PCA reduceert dimensies door zoveel mogelijk variatie te behouden. De som van de uitgelegde variantie van de gekozen componenten bepaalt hoeveel informatie behouden blijft.

Waarom de PCA Gebruiken?

1. Dimensiereductie:
   • Vermindert het aantal kenmerken, wat de rekentijd en het geheugengebruik verlaagt.
   • Vermindert ruis in data en verbetert de prestaties van machine learning-modellen.
2. Visualisatie:
   • Helpt complexe datasets met veel dimensies te visualiseren in 2D of 3D.
3. Feature Extractie:
   • Vereenvoudigt de data-analyse door de meest significante kenmerken te identificeren.

Toepassingen van PCA

• Beeldverwerking: Compressie en ruisreductie in afbeeldingen.
• Financiële Analyse: Identificatie van belangrijke marktfactoren en trends.
• Marketing: Klantsegmentatie door het samenvatten van gedragsgegevens.
• Genetica: Reduceren van de dimensies van genexpressiedata.

Voorbeeld van een PCA

Stel je hebt een dataset met drie kenmerken: inkomen, leeftijd, en uitgaven. Door PCA toe te passen, worden deze drie kenmerken samengevat in twee principiële componenten die 90% van de variantie verklaren. Hiermee kun je eenvoudig analyses uitvoeren en patronen ontdekken zonder informatie overbodig te maken. Onderstaand een voorbeeld van de visualisatie van de dataset, gereduceerd tot twee principale componenten (PC1 en PC2) met behulp van PCA.

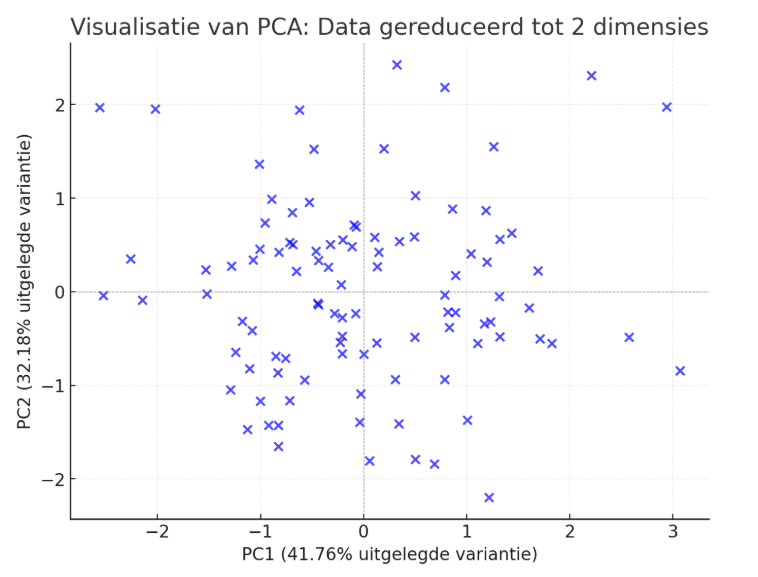
Analyse van de Resultaten:

• PC1 (41.76%): Verklaart het grootste deel van de variantie in de data.
• PC2 (32.18%): Verklaart een significant deel van de resterende variantie.

Samen verklaren deze twee componenten ongeveer 73.94% van de totale variantie in de dataset. Dit betekent dat de meeste informatie uit de originele data behouden blijft in deze reductie.

Welke kanttekeningen kunnen worden geplaatst bij de PCA?

Hoewel PCA een krachtige techniek is, zijn er enkele kanttekeningen en beperkingen waar rekening mee moet worden gehouden bij het gebruik ervan:

1. Verlies van interpretatie

• Probleem: PCA transformeert de originele kenmerken in lineaire combinaties (principale componenten), die vaak geen duidelijke fysieke of praktische betekenis hebben.
• Gevolg: Het kan moeilijk zijn om de resultaten te interpreteren, vooral in domeinen waar inzicht in de relatie tussen kenmerken belangrijk is.

2. Gevoeligheid voor schaal

• Probleem: PCA is gevoelig voor de schaal van de variabelen. Als variabelen verschillende eenheden hebben (bijv. leeftijd in jaren en inkomen in euro’s), zullen kenmerken met grotere variaties domineren.
• Oplossing: Normalisatie of standaardisatie van de data vóór PCA is essentieel.

3. Lineariteit

• Probleem: PCA gaat ervan uit dat relaties tussen variabelen lineair zijn. Als de onderliggende patronen in de data niet-lineair zijn, zal PCA deze mogelijk niet goed vastleggen.
• Oplossing: Voor niet-lineaire patronen kunnen alternatieven zoals Kernel PCA of t-SNE worden overwogen.

4. Geen garantie voor betekenisvolle dimensies

• Probleem: Hoewel PCA zich richt op het behouden van maximale variantie, is er geen garantie dat de gereduceerde dimensies daadwerkelijk de meest relevante of nuttige informatie bevatten voor een specifiek probleem.
• Gevolg: PCA kan informatie behouden die voor een specifieke toepassing onbelangrijk is, terwijl kritieke informatie verloren gaat.

5. Gevoeligheid voor ruis

• Probleem: PCA probeert zoveel mogelijk variantie te behouden, maar maakt geen onderscheid tussen bruikbare en ruisvariantie.
• Gevolg: Bij datasets met veel ruis kan PCA ruis opnemen in de principale componenten.

6. Vereiste van lineair onafhankelijke kenmerken

• Probleem: Als er sterke multicollineariteit is (kenmerken zijn sterk gecorreleerd), kunnen sommige componenten overlappen in betekenis. Dit kan leiden tot redundantie in de gereduceerde data.
• Oplossing: PCA werkt het beste als er weinig correlatie tussen de originele kenmerken is.

7. Geen robuustheid tegen uitbijters

• Probleem: PCA is gevoelig voor uitbijters, omdat deze de covariantiematrix en de berekening van eigenvectoren sterk kunnen beïnvloeden.
• Oplossing: Voorbehandeling van de data om uitbijters te verwijderen of robuuste PCA-methoden te gebruiken.

8. Vereist voldoende data

• Probleem: PCA werkt minder goed bij kleine datasets of datasets met een lage verhouding tussen observaties en kenmerken. De resultaten kunnen instabiel of niet representatief zijn.
• Gevolg: PCA kan overmatig ruisgevoelig zijn bij een gebrek aan voldoende data.

9. Uitleg van de variantie kan onvolledig zijn

• Probleem: Zelfs met PCA kan een groot deel van de variantie in de data worden genegeerd als de eerste componenten slechts een klein percentage van de variantie verklaren.
• Gevolg: Er kunnen meer componenten nodig zijn, wat het voordeel van dimensiereductie beperkt.

10. Niet geschikt voor categorische data

• Probleem: PCA werkt alleen met numerieke data en is niet direct toepasbaar op categorische of nominale gegevens.
• Oplossing: Encoding-technieken zoals one-hot encoding moeten eerst worden toegepast, maar dit kan de dimensie verhogen in plaats van verlagen.

Conclusie

PCA is nuttig voor dimensiereductie en patroonherkenning, maar het is niet altijd geschikt of voldoende voor alle datasets of toepassingen. Begrijpen wanneer PCA wel of niet effectief is, en de data goed voorbereiden, zijn cruciaal voor het succes van de methode. Voor sommige problemen kunnen alternatieve technieken zoals t-SNE, UMAP, of domeinspecifieke modellen betere resultaten bieden.

LITERATUUR

1. Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press.
2. Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction (2nd ed.). Springer.
3. Jolliffe, I. T. (2002). Principal Component Analysis (2nd ed.). Springer.