Hidden Markov Model (HMM) betreft een statistisch model dat wordt gebruikt om systemen te beschrijven die evolueren over de tijd op een manier die wordt gekarakteriseerd door een reeks verborgen toestanden (staten) en waar de observaties van deze toestanden stochastisch zijn, ofwel toevalsvariabelen kennen. In meer wetenschappelijke termen is een HMM een speciaal geval van een Markov-keten, waarbij de werkelijke toestand van het systeem niet direct waarneembaar (verborgen) is, echter wel indirect kan worden afgeleid door de observatie van bepaalde waarneembare signalen (emissies).
Definitie Hidden Markov Model
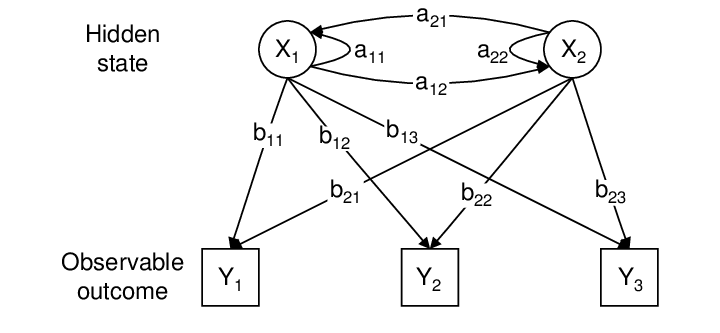
Een Hidden Markov Model kan formeel worden gedefinieerd door de navolgende vijf componenten:
- N: Het aantal verborgen toestanden in het model.
- M: Het aantal verschillende observaties dat mogelijk is, dat wil zeggen de verschillende output-symbolen die kunnen worden waargenomen.
- A: De toestands-overgangs-matrix, waarbij Aij de kans is om van toestand i naar toestand j te gaan.
- B: De emissie-matrix, waarbij Bj(k) de kans is dat observatie k wordt gezien gegeven dat het systeem zich in toestand j bevindt.
- π\piπ: De initiële toestandsdistributie, oftewel de waarschijnlijkheid dat het systeem zich initieel in een bepaalde toestand bevindt.
Markov-eigenschap
Een van de belangrijkste aannames in een HMM betreft de Markov-eigenschap: de toestand op tijdstip t hangt alleen af van de toestand op tijdstip t−1, en niet van eerdere toestanden. Dit wordt de “first-order” Markov-eigenschap genoemd.
Creativiteit en innovatiekracht ontwikkelen voor uw organisatie?
De aandachtsspanne van de consument is schaars. Om de consument van vandaag de dag te overtuigen van uw product of dienst, is toegevoegde waarde en onderscheidend vermogen erg belangrijk. Lees meer →

Toepassingen van Hidden Markov Models
- Spraakherkenning: HMM’s worden op grote schaal gebruikt in spraakherkenning. Hierbij worden de spraakgeluiden als een reeks waarnemingen beschouwd, en het HMM-model probeert de reeks van verborgen fonemen (spraakgeluiden) af te leiden op basis van deze waarnemingen. Elke fonem wordt gemodelleerd als een verborgen toestand, en de werkelijke uitgesproken geluiden vormen de observaties.
- Voorbeeld: Google’s spraak-naar-tekst functie gebruikt HMM’s om spraakpatronen te herkennen en om te zetten naar tekst.
- Voorbeeld: Google’s spraak-naar-tekst functie gebruikt HMM’s om spraakpatronen te herkennen en om te zetten naar tekst.
- DNA-sequentie-analyse: In de bio-informatica worden HMM’s gebruikt om DNA-sequenties te analyseren. Verschillende delen van het DNA kunnen worden beschouwd als verborgen toestanden (bijv. coderende of niet-coderende regio’s), terwijl de nucleotiden de waargenomen signalen zijn.
- Voorbeeld: Het identificeren van genen in lange DNA-sequenties gebeurt vaak met behulp van HMM’s om te bepalen of een segment van de sequentie een coderende regio is.
- Voorbeeld: Het identificeren van genen in lange DNA-sequenties gebeurt vaak met behulp van HMM’s om te bepalen of een segment van de sequentie een coderende regio is.
- Beurskoersen modelleren: HMM’s worden ook gebruikt om financiële tijdreeksen, zoals beurskoersen, te modelleren. De verborgen toestanden kunnen marktfactoren of sentimenten representeren die niet direct waarneembaar zijn, terwijl de waargenomen data de prijsschommelingen zijn.
- Voorbeeld: In financieel risicobeheer kunnen HMM’s worden gebruikt om toekomstige bewegingen van aandelenkoersen te voorspellen door verborgen marktfactoren te modelleren.
Literatuur inzake HMM’s
HMM’s zijn uitvoerig beschreven, ondermeer in het werk van L. E. Baum en T. Petrie in 1966, waarin ze een probabilistisch model formuleerden voor het beschrijven van sequentiële gegevens. Daarnaast zijn de werken van Rabiner (1989) cruciaal, die HMM’s populariseerde in de context van spraakherkenning en gedetailleerd uitlegde hoe de algoritmen voor parameter-schattingsproblemen (zoals het Baum-Welch algoritme) werken.
Voorbeelden van algoritmen binnen HMM’s
- Forward-backward algoritme: Gebruikt om de waarschijnlijkheid van een bepaalde reeks waarnemingen te berekenen, gegeven een HMM.
- Viterbi-algoritme: Gebruikt om de meest waarschijnlijke reeks verborgen toestanden te bepalen, gegeven een reeks waarnemingen.
- Baum-Welch algoritme: Gebruikt voor parameterestimatie binnen een HMM. Dit is een speciale vorm van het Expectation-Maximization (EM) algoritme.
Welke kanttekeningen kunnen worden geplaatst bij HMM’s?
Binnen de wetenschappelijke literatuur worden verschillende kritische kanttekeningen geplaatst bij het gebruik van Hidden Markov Models (HMM), ondanks de wijdverbreide toepassingen en bruikbaarheid. Onderstaand enkele van de belangrijkste punten van kritiek en beperkingen die in de literatuur worden weergegeven.
1. Beperkte expressiviteit van het model
Een van de fundamentele kritiekpunten is dat HMM’s beperkte expressiviteit hebben door hun first-order Markov-eigenschap. Dit betekent dat elke verborgen toestand alleen afhankelijk is van de vorige toestand, wat vaak een te eenvoudige weergave is van complexe, real-world sequenties:
- Kritiekpunt: Veel systemen in de natuur of technologie hebben lange-termijn afhankelijkheden waarbij toekomstige toestanden afhangen van eerdere toestanden verder terug in de tijd. HMM’s zijn slecht uitgerust om zulke lange-termijn relaties vast te leggen.
- Oplossingen: Alternatieven zoals higher-order Markov models of Long Short-Term Memory (LSTM) netwerken in deep learning kunnen dergelijke lange-termijnafhankelijkheden beter modelleren.
2. Vereenvoudigde aannames over emissie- en transitiekansen
De aannames binnen HMM’s over de transitiekansen tussen toestanden en de emissiekansen (waarnemingen gegeven een toestand) worden vaak als te rigide en simplistisch beschouwd:
- Kritiekpunt: HMM’s gaan uit van stationaire waarschijnlijkheidsverdelingen, wat betekent dat de overgangs- en emissiematrices constant blijven over de tijd. In werkelijkheid kunnen deze probabiliteiten echter variëren, bijvoorbeeld door externe factoren of veranderende dynamieken in het systeem.
- Oplossingen: Methoden zoals Switching Hidden Markov Models (SHMMs) of Time-Varying HMMs zijn ontwikkeld om met deze tijdsvariërende kansen om te gaan.
3. Vooropgestelde aantal toestanden en observaties
In HMM’s moet het aantal toestanden (NNN) en observaties (MMM) vooraf worden gedefinieerd, wat kan leiden tot modelmatige bias:
- Kritiekpunt: Het vooraf bepalen van het aantal toestanden kan problematisch zijn als er onvoldoende kennis is over het systeem. Te weinig toestanden kunnen leiden tot onderspecificatie van het model, terwijl te veel toestanden kunnen leiden tot overfitting.
- Oplossingen: Modellen zoals de Infinite Hidden Markov Model (iHMM), gebaseerd op Dirichlet Processen, maken het mogelijk om het aantal toestanden adaptief te laten variëren op basis van de data.
4. Overfitting en generalisatieproblemen
HMM’s kunnen gevoelig zijn voor overfitting, vooral wanneer ze worden toegepast op kleine datasets:
- Kritiekpunt: Als de parameters van een HMM worden geschat op basis van beperkte of ruisgevoelige data, kan het model te veel “leren” van de specifieke eigenschappen van de trainingsdata, wat de generalisatie naar nieuwe data beperkt.
- Oplossingen: Regulatie-technieken zoals Bayesian HMMs voegen een probabilistische prior toe aan de parameters van het model, wat het risico op overfitting vermindert. Ook kan cross-validation helpen om een betere balans te vinden tussen bias en variantie.
5. Berekeningsintensiteit en schaalbaarheid
Hoewel de basisalgoritmen voor HMM’s zoals Baum-Welch en Viterbi efficiënt zijn, kunnen HMM’s onpraktisch worden wanneer ze worden toegepast op zeer grote datasets of op systemen met een groot aantal toestanden:
- Kritiekpunt: De computationele kosten voor het uitvoeren van inference en parameteroptimalisatie schalen kwadratisch met het aantal toestanden en de lengte van de observatiesequentie. Voor grote modellen kan dit leiden tot aanzienlijke rekentijd en geheugenvereisten.
- Oplossingen: Parallelle computing en algoritmische optimalisaties zijn onderzocht om deze schaalbaarheidsproblemen aan te pakken. Bovendien bieden Approximate Inference-technieken zoals variational methods snellere benaderingen om HMM-parameters te schatten.
6. Deterministische aannames in een stochastisch model
Een ander punt van kritiek betreft het feit dat HMM’s proberen een complex stochastisch proces te modelleren met een vrij eenvoudige stochastische structuur:
- Kritiekpunt: De observaties zijn afhankelijk van een enkele verborgen toestand, wat vaak niet voldoende is om complexe systemen adequaat te beschrijven. In real-world situaties kunnen meerdere factoren een rol spelen bij het genereren van een waarneming, en HMM’s gaan hier te simplistisch mee om.
- Oplossingen: Modellen zoals Factorial HMMs kunnen worden gebruikt om meerdere verborgen toestanden tegelijk te modelleren en zo complexere afhankelijkheden te vertegenwoordigen.
7. Interpretatie van de toestanden
Hoewel HMM’s verborgen toestanden modelleren, is er frequent kritiek op de interpretatie van deze toestanden:
- Kritiekpunt: In veel toepassingen, zoals spraakherkenning of bio-informatica, is het moeilijk om de werkelijke betekenis van de verborgen toestanden intuïtief te interpreteren. De toestanden zijn vaak abstract en geven geen duidelijke of tastbare informatie over de aard van het systeem.
- Oplossingen: Door hybride modellen zoals discriminatieve modellen te combineren met HMM’s, kunnen de verborgen toestanden in een HMM beter geïnterpreteerd worden. Ook kan gebruik van domain knowledge helpen om betekenisvolle interpretaties aan de toestanden te koppelen.
8. Geen flexibiliteit in modellering van niet-lineaire dynamieken
Een andere beperking van HMM’s is hun onvermogen om niet-lineaire dynamieken in data te modelleren:
- Kritiekpunt: Veel real-world systemen vertonen niet-lineair gedrag, maar HMM’s zijn in wezen lineaire modellen. Dit maakt ze minder geschikt voor toepassingen waar niet-lineaire transities of complexere dynamieken in de toestandsveranderingen een rol spelen.
- Oplossingen: Modellen zoals Hidden Semi-Markov Models (HSMMs) of Kalman-filters kunnen worden gebruikt om niet-lineaire relaties beter te modelleren.
LITERATUUR
- Baum, L. E., & Petrie, T. (1966). “Statistical Inference for Probabilistic Functions of Finite State Markov Chains.” The Annals of Mathematical Statistics, 37(6), 1554-1563.
- Rabiner, L. R. (1989). “A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition.” Proceedings of the IEEE, 77(2), 257-286.
- Beal, M. J., & Ghahramani, Z. (2001). “The Infinite Hidden Markov Model.” Advances in Neural Information Processing Systems (NIPS), 14.
- Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.
Winstgevendheid verhogen en uw bedrijf in waarde laten toenemen?
UBS Business Value Creation Services ondersteunt organisaties bij het verhogen van winst- en bedrijfswaarde. Ons team focust zich hierbij op domeinen die de grootste impact hebben op het bedrijfsresultaat. Lees meer →








Reageer op dit bericht