Stochastisch Model van Miller en Orr

Het model van Miller en Orr (1966), ook wel bekend als het Miller-Orr Model, betreft een stochastisch model voor kasbeheer (cashmanagement) dat bedrijven helpt om hun liquiditeitspositie efficiënt en effectief te beheren. Het model is met name geschikt voor ondernemingen met onvoorspelbare inkomende en uitgaande kasstromen, en biedt houvast voor het bepalen van optimale kasreserves.

Miller en Orr bouwden voort op het werk van Baumol (1952), welke een deterministisch model voor kasbeheer ontwikkelde dat vergelijkbaar was met de klassieke economische bestelhoeveelheid (EOQ)-formule. In tegenstelling tot Baumols model, dat uitgaat van voorspelbare kasstromen, introduceerden Miller en Orr een stochastische benadering, waarbij het kasniveau zich willekeurig beweegt volgens een Brownse beweging.

Veronderstellingen van het model

Het model van Miller en Orr is gebaseerd op de navolgende aannames:

1. Kasstromen volgen een Brownse beweging: De dagelijkse kasstromen worden willekeurig gegenereerd en hebben een constante gemiddelde variantie (σ2\sigma^2σ2).
2. Transactiekosten en opportunitykosten zijn bekend: Het model werkt optimaal als de kosten voor het verhandelen van effecten en het mislopen van rendement goed gekwantificeerd kunnen worden.
3. Er is altijd toegang tot kortetermijnbeleggingen: Het bedrijf dient in staat te zijn om direct geld te investeren of op te nemen.
4. Er zijn geen restricties op liquiditeitsbeheer: Er zijn geen wettelijke of operationele beperkingen op hoe vaak en hoeveel geld kan worden opgenomen of belegd.

Werking van het model

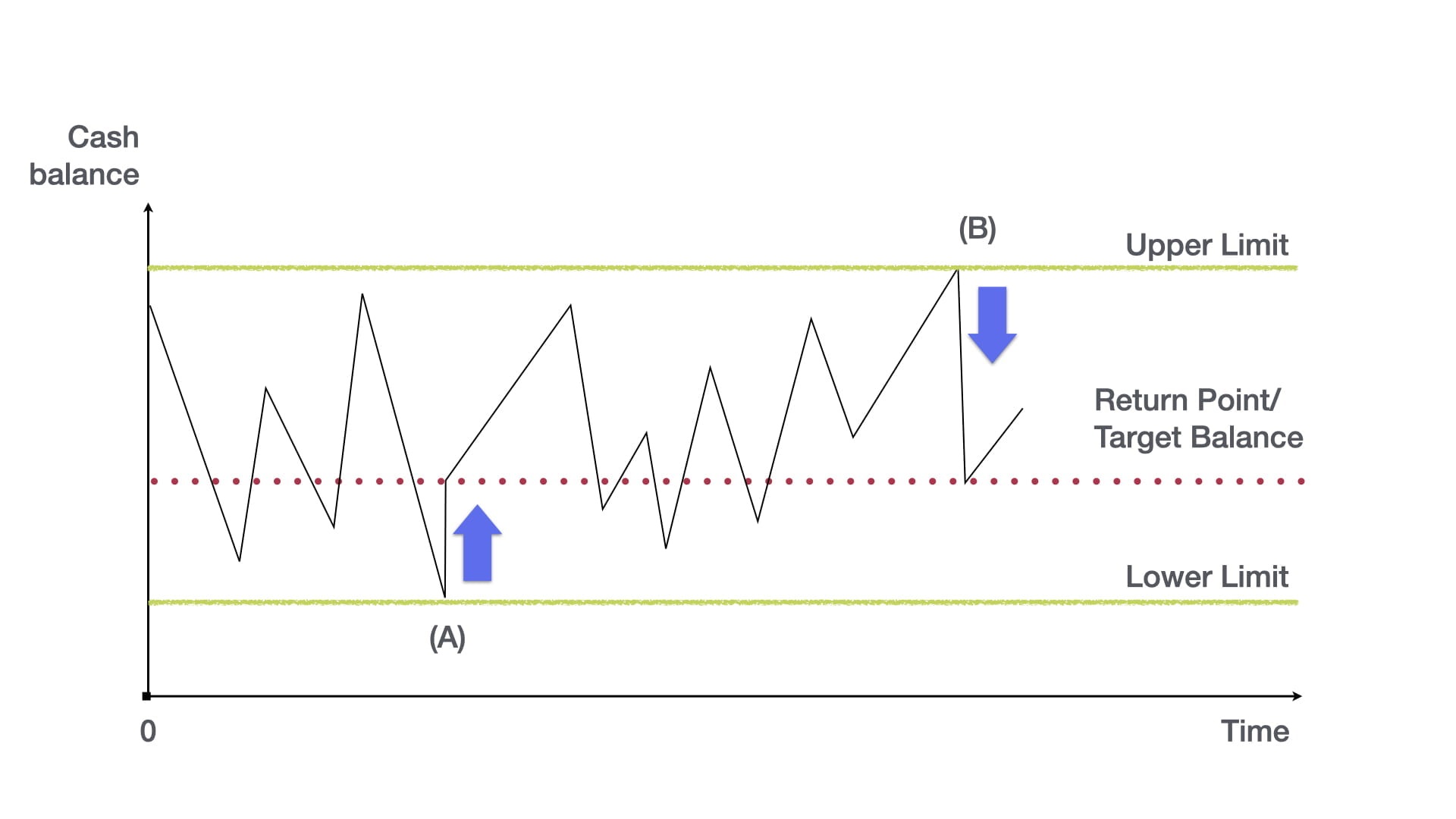
Het model veronderstelt dat de dagelijkse kasstromen van een bedrijf willekeurig variëren, wat leidt tot fluctuaties in het kassaldo. De kern van het model is het instellen van een boven- en ondergrens voor de kasreserves, met een daartussen gelegen doelniveau waarnaar het saldo telkens terugkeert zodra een grens wordt bereikt.

1.1. Drie kerncomponenten van het model

• Bovengrens (U): Wanneer het kassaldo deze limiet bereikt, investeert het bedrijf het overtollige geld in kortlopende effecten of andere beleggingen om rendement te genereren.
• Ondergrens (L): Wanneer het kassaldo deze limiet bereikt, verkoopt het bedrijf effecten of haalt extra financiering op om het saldo weer aan te vullen.
• Doelniveau (Z): Dit is het niveau waaraan het kassaldo na een aanpassing wordt teruggebracht. Dit niveau ligt dichter bij de ondergrens dan bij de bovengrens.

De wiskundige grondslag

Het model berekent de optimale afstand tussen de boven- en ondergrens door middel van de  navolgende formule:

$U\; –L=3\times {\left(\frac{3·b·{\sigma }^2}{4·r}\right)}^{\frac{1}{3}}$

waarbij:

• b = transactiekosten per aanpassing (bijv. kosten voor het kopen of verkopen van effecten).
• σ² = variantie van de dagelijkse kasstromen.
• r = opportunity cost van het aanhouden van liquide middelen (bijv. gemiste renteopbrengsten).

Het doelniveau wordt bepaald als:

$Z=L+\frac{1}{3}\times \left(U,–,L\right)$

Hieruit blijkt dat het kassaldo na elke aanpassing terugkeert naar een niveau dat dichter bij de ondergrens ligt dan bij de bovengrens. Dit minimaliseert de kosten van kasbeheer.

Welke kanttekeningen kunnen bij het model worden geplaatst?

Hoewel het model van Miller en Orr overwegend enorm zinvol is, zijn er enkele kanttekeningen bij het model te plaatsen: 

1. Aannames kunnen onrealistisch zijn

• In de praktijk volgen kasstromen niet altijd een zuivere Brownse beweging. Er kunnen schokken optreden door macro-economische factoren, seizoensinvloeden of bedrijfsspecifieke gebeurtenissen.
• Niet alle bedrijven hebben directe toegang tot liquide investeringen die zonder frictiekosten kunnen worden gekocht of verkocht.

2. Beperkte toepasbaarheid voor langetermijnkapitaalbeheer

• Het model richt zich primair op kortetermijnkasbeheer en is minder geschikt voor sectoren met langdurige investeringscycli, zoals vastgoed en infrastructuur.

3. Gevoeligheid voor inputparameters

• De optimale grenzen hangen sterk af van de nauwkeurigheid van de schattingen van σ²,b en r.
• Kleine schommelingen in deze parameters kunnen leiden tot suboptimale beslissingen.

LITERATUUR

1. Miller, M. H., & Orr, D. (1966). A Model of the Demand for Money by Firms. The Quarterly Journal of Economics, 80(3), 413-435. 
2. Baumol, W. J. (1952). The Transactions Demand for Cash: An Inventory Theoretic Approach. The Quarterly Journal of Economics, 66(4), 545-556. 
3. Ross, S. A., Westerfield, R. W., & Jaffe, J. (2016). Corporate Finance (11th ed.). McGraw-Hill Education.
4. Tirole, J. (2006). The Theory of Corporate Finance. Princeton University Press.