Het Black-Litterman-model

Het Black-Litterman-model, ontwikkeld door Fischer Black en Robert Litterman (1992) bij Goldman Sachs, betreft een kwantitatief beleggingsmodel dat de klassieke mean-variance optimization (Markowitz, 1952) uitbreidt door subjectieve marktinzichten van beleggers te combineren met marktimpliciete rendementen. Het doel is een stabielere, beter gespreide portefeuilleconstructie die minder gevoelig is voor inputfouten (zoals verwachte rendementen) ten opzichte van traditionele modellen (Satchell & Scowcroft, 2000).

Probleem met klassieke Markowitz-optimalisatie

Het traditionele Markowitz-model vereist dat beleggers verwachte rendementen, covarianties en varianties van activa schatten. In de praktijk:

• Kleine veranderingen in verwachte rendementen leiden tot substantiële  verschuivingen in portefeuillesamenstelling (Michaud, 1989).
• Inputfouten resulteren veelal in onrealistische en geconcentreerde portefeuilles.

Het Black-Litterman-model adresseert dit door een Bayesiaanse benadering, waarbij de verwachte rendementen worden afgeleid uit evenwichtsveronderstellingen en vervolgens aangepast worden op grond van beleggersvoorkeuren (views).

Creativiteit en innovatiekracht ontwikkelen voor uw organisatie?

De aandachtsspanne van de consument is schaars. Om de consument van vandaag de dag te overtuigen van uw product of dienst, is toegevoegde waarde en onderscheidend vermogen erg belangrijk. Lees meer →

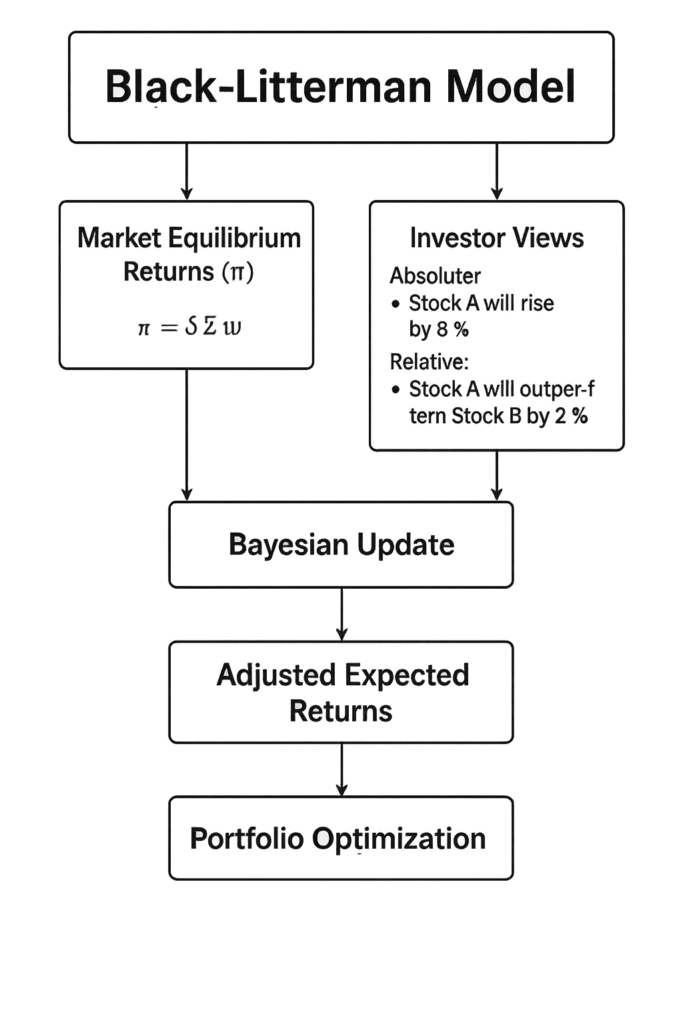
Kernstructuur van het Black-Litterman-model

Het Black-Litterman-model combineert twee kerncomponenten (Black & Litterman, 1992):

1. Marktevenwichtsrendementen (π)
Deze worden afgeleid uit marktkapitalisatiegewichten (`w`), de covariantiematrix (`Σ`) en een risicobereidheidsparameter (`δ`): \[ \pi = \delta \Sigma w \]

Hierbij geldt:
– `δ` = risicobereidheidsparameter (afgeleid uit het marktrisicoprofiel)
– `Σ` = covariantiematrix van activa
– `w` = marktgewichten (bijvoorbeeld MSCI-indexgewichten)

Dit levert de impliciete verwachte rendementen zoals afgeleid uit de markt.

2. Beleggersinzichten (views)
Beleggers geven verwachtingen aan over individuele activa of combinaties (relatief of absoluut). Deze worden vastgelegd met:
– `P`: een matrix die aangeeft op welke activa de views betrekking hebben
– `q`: de verwachte rendementen volgens de views
– `Ω`: de onzekerheidsmatrix van deze views

3. Bayesiaanse combinatie
De marktverwachtingen (`π`) en beleggersinzichten (`q`) worden gecombineerd via een Bayesiaanse update: \[ E[R] = \Big[(\tau\Sigma)^{-1} + P’\Omega^{-1}P\Big]^{-1} \Big[(\tau\Sigma)^{-1}\pi + P’\Omega^{-1}q\Big] \]Waarbij:
– `τ` = schaalfactor die de onzekerheid in evenwichtsverwachtingen weerspiegelt
– `E[R]` = aangepaste verwachte rendementen die consistent zijn met zowel de markt als de beleggersinzichten

4. Optimalisatie
De aangepaste rendementen `E[R]` worden vervolgens gebruikt in een klassieke *mean-variance optimization* om de uiteindelijke portefeuillegewichten te bepalen.

Winstgevendheid verhogen en uw bedrijf in waarde laten toenemen?

UBS Business Value Creation Services ondersteunt organisaties bij het verhogen van winst- en bedrijfswaarde. Ons team focust zich hierbij op domeinen die de grootste impact hebben op het bedrijfsresultaat. Lees meer →

Toepassing in de praktijk

1. Bepaal marktinput
   • Verzamel marktkapitalisatiegewichten (bijv. wereldwijde indices) en de covariantiematrix.
   • Bereken de impliciete marktverwachtingen (π) met de bovengenoemde formule.
     
2. Formuleer beleggersinzichten
   • Leg vast welke activa of sectoren over- of onderpresteren, inclusief een inschatting van de onzekerheid (Ω).
   • Vertaal deze verwachtingen in matrixvorm (P en q).
     
3. Combineer markt en inzichten (Bayesiaanse update)
   • Gebruik de Black-Litterman-formule om de nieuwe verwachte rendementen te berekenen.
     
4. Optimaliseer de portefeuille
   • Pas de standaard mean-variance optimalisatie toe met de aangepaste rendementen, rekening houdend met risicovoorkeur en beperkingen (bijvoorbeeld maximumwegingen).
     
5. Evaluatie en herijking
   • Voer stress tests en scenarioanalyses uit, herhaal periodiek met nieuwe views.
     

Welke kanttekeningen kunnen worden geplaatst bij het Black-Litterman-model?

Alhoewel het een sterk en zinvol model betreft, zijn er enkele kanttekeningen te plaatsen:

1. Complexiteit en implementatie
   Het model vereist geavanceerde kwantitatieve kennis (Bayesiaanse statistiek, matrixalgebra) en is daardoor minder toegankelijk voor kleinere beleggers (Meucci, 2009).
   
2. Gevoeligheid voor parameters
   Keuzes zoals de schaalfactor τττ en de onzekerheid in views (Ω) zijn subjectief en hebben grote impact op het eindresultaat (Idzorek, 2007).
   
3. Aanname van normale verdeling
   Het model veronderstelt dat rendementen normaal verdeeld zijn en dat markten in evenwicht zijn, wat niet altijd empirisch standhoudt (Michaud et al., 2013).
   
4. Beperkte bruikbaarheid bij illiquide of niet-genoteerde activa
   Omdat het model leunt op marktkapitalisatie en covariantie, is toepassing op private equity of vastgoed beperkt.

Conclusie

Het Black-Litterman-model is een krachtig instrument dat de instabiliteit van klassieke portefeuilles minimaliseert door marktinformatie en beleggersinzichten te combineren. Het is vooral geschikt voor institutionele beleggers die hun marktexposure willen verfijnen met subjectieve verwachtingen. De bruikbaarheid hangt echter sterk af van de kwaliteit van de input, de aannames over onzekerheden, en de expertise van de gebruiker.

LITERATUUR

1. Black, F., & Litterman, R. (1992). Global portfolio optimization. Financial Analysts Journal, 48(5), 28–43. 
2. Idzorek, T. M. (2007). A step-by-step guide to the Black-Litterman model. Zephyr Associates.
3. Meucci, A. (2009). Managing diversification. Risk, 22(5), 74–79.
4. Michaud, R. O. (1989). The Markowitz optimization enigma: Is ‘optimized’ optimal? Financial Analysts Journal, 45(1), 31–42.
5. Michaud, R. O., Esch, D. N., & Michaud, R. (2013). Efficient asset management: A practical guide to stock portfolio optimization and asset allocation (2nd ed.). Oxford University Press.
6. Satchell, S., & Scowcroft, A. (2000). A demystification of the Black-Litterman model: Managing quantitative and traditional portfolio construction. Journal of Asset Management, 1(2), 138–150.

Winstgevendheid verhogen en uw bedrijf in waarde laten toenemen?

UBS Business Value Creation Services ondersteunt organisaties bij het verhogen van winst- en bedrijfswaarde. Ons team focust zich hierbij op domeinen die de grootste impact hebben op het bedrijfsresultaat. Lees meer →