Het Black Scholes Model: Waardering van financiële opties

Het Black Scholes model, ontwikkeld door Fischer Black, Myron Scholes en Robert Merton in 1973, betreft een wiskundig model dat de theoretische prijs van Europese stijl opties berekent. Dit model heeft een aanzienlijke invloed gehad op de financiële wereld en wordt veelvuldig gebruikt om optieprijzen te bepalen. 

Fundamenten van het Black Scholes Model

Het model is gebaseerd op een aantal aannames, waaronder:

1. Constante volatiliteit (σ)
Volatiliteit, de mate van prijsschommelingen van een financieel instrument, wordt in het Black-Scholes-model als constant beschouwd gedurende de levensduur van de optie. Dit impliceert dat de volatiliteit een cruciale factor is bij het bepalen van de optieprijzen.

2. Continue prijsbewegingen
Het model veronderstelt dat de prijs van het onderliggende actief een continue stochastische beweging volgt. Deze continue beweging wordt gemodelleerd met behulp van geometrische Brownse beweging, waardoor het model geschikt is voor het beschrijven van de dynamiek van financiële markten.

3. Geen dividenden
Een van de aannames van het Black-Scholes-model is dat het onderliggende actief gedurende de looptijd van de optie geen dividenden uitkeert. Deze vereenvoudiging vergemakkelijkt de wiskundige formulering van het model.

4. Risicovrije rente (r)
Het model veronderstelt dat investeerders hun geld risicovrij kunnen beleggen tegen de risicovrije rente. Dit houdt in dat de rentevoet een constante is gedurende de levensduur van de optie.

Black Scholes formules

De formules voor de Europese call-optie (C) en put-optie (P) zijn essentieel voor het model.

Voor een call-optie geldt:

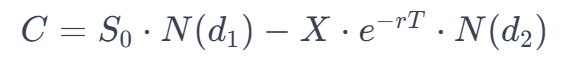
En voor een put-optie geldt:

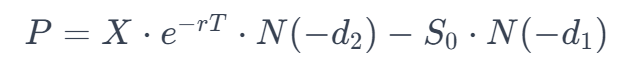
Waarbij:

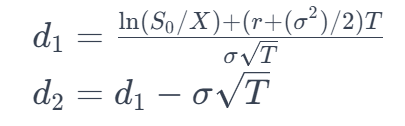
Rekenvoorbeeld:

Om de (theoretische) prijzen van een call-optie (C) en put-optie (P) te illustreren, laten we een voorbeeld nemen met het navolgende:

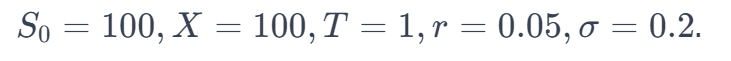
1. Bereken d1​ en d2​ (d1=0.35 en d2 =0.15)
2. Gebruik N (cumulatieve normale verdelingsfunctie) waarden om C en P te berekenen.
3. Substitueer deze waarden in de formules om de theoretische prijzen te verkrijgen.

Voorgenoemd voorbeeld illustreert de toepassing van het Black-Scholes-model in het bepalen van optieprijzen op basis van verschillende financiële parameters.

Kanttekeningen bij het Black Scholes Model

Hoewel het Black-Scholes-model een krachtig instrument is voor het waarderen van financiële opties, zijn er enkele belangrijke kanttekeningen en beperkingen die men in overweging dient te nemen:

1. Aannames:
   • Het model is gebaseerd op verschillende aannames, zoals constante volatiliteit, continue prijsbewegingen, geen dividenden en risicovrije rente. In de praktijk kunnen deze aannames vaak niet volledig worden nageleefd, wat de nauwkeurigheid van de voorspellingen kan beïnvloeden.
     
2. Niet toepasbaar op alle soorten opties:
   • Het Black-Scholes-model is specifiek ontworpen voor Europese stijl opties, die alleen op de vervaldatum kunnen worden uitgeoefend. Amerikaanse stijl opties, die op elk moment vóór de vervaldatum kunnen worden uitgeoefend, vereisen aanpassingen aan het model.
     
3. Volatiliteitsschommelingen:
   • Hoewel volatiliteit als constant wordt aangenomen, kan deze in werkelijkheid variëren. Bij plotselinge veranderingen in volatiliteit kan het model de optieprijzen mogelijk niet nauwkeurig voorspellen.
     
4. Dividenduitkeringen:
   • Het model houdt geen rekening met dividenden op het onderliggende actief, wat een beperking is bij het waarderen van opties op aandelen die regelmatig dividenden uitkeren.
     
5. Risicovrije rente:
   • De aanname van een constante risicovrije rente kan problematisch zijn, vooral in economische omgevingen met aanzienlijke renteschommelingen.
     
6. Korte-termijnopties en extreme gebeurtenissen:
   • Voor zeer korte-termijnopties of in tijden van extreme marktgebeurtenissen, kan het Black-Scholes-model minder effectief zijn.
     
7. Gebrek aan liquiditeit:
   • Het model gaat ervan uit dat de markt voldoende liquide is, wat betekent dat er genoeg kopers en verkopers zijn om tegen redelijke prijzen te handelen. In illiquide markten kan het model minder betrouwbaar zijn.
     
8. Gebaseerd op historische gegevens:
   • Het model gebruikt historische gegevens om volatiliteit te schatten. In snel veranderende marktomstandigheden kan deze schatting mogelijk achterhaald zijn.

Inzicht in deze kanttekeningen is cruciaal om bewust te zijn van de beperkingen van het Black-Scholes-model. Voor complexere scenario’s en omstandigheden kunnen andere modellen, zoals het Binomiale Optiemodel of Monte Carlo-simulaties, meer geschikt zijn. Het blijft belangrijk om de context en specifieke omstandigheden van de markt in overweging te nemen bij het gebruik van financiële modellen.

LITERATUUR
Black, Fischer; Scholes, Myron (1973). “The Pricing of Options and Corporate Liabilities”. Journal of Political Economy. 81 (3): 637–654.